DC Arc Flash

Abstract:

As the integration of renewable energy sources like Battery Energy Storage Systems (BESS) and Photovoltaic (PV) systems becomes increasingly prevalent, understanding and mitigating the risks associated with DC arc flash incidents is critical. DC arc flash hazards present unique challenges compared to their AC counterparts, primarily due to the continuous nature of DC current, which can sustain arcs for longer periods. This article delves into the mechanisms of DC arc flash within BESS and PV systems, highlighting the factors that influence arc flash severity, such as short-circuit currents, system voltage, and conductor spacing. We explore the methodologies for calculating incident energy and arc flash boundaries, with a focus on the standards and equations used in DC systems. Through detailed analysis and practical examples, this article aims to provide a comprehensive understanding of DC arc flash risks in the context of modern renewable energy installations. In this first article, we will specifically discuss DC arc flash risks in PV systems, providing a detailed analysis and practical examples to enhance safety in modern renewable energy installations.

1. Introduction:

Increasing exposure to DC systems results in increased chances of personnel injury from DC electrical hazards, including arc flash. In 2018, IEEE Std 1584 – IEEE Guide for Performing Arc-Flash Hazard Calculations, saw revisions that completely changed the standard based upon additional testing performed to address inadequacies in the empirically derived model. However, this update did not include single phase AC or DC arc flash, thereby leaving NFPA 70E Standard for Electrical Safety in the Workplace, to address DC arc flash electrical hazard [1].

Direct current (DC) networks and systems are becoming more and more widespread. The number of DC systems has been rising for years, but DC supply systems in connection with energy storage systems, high-voltage batteries for vehicles, DC drives, DC smart grids etc. are also becoming increasingly important. In many cases these are systems in the low voltage range (up to 1500 V). In addition, such systems often have high power ratings. In the event of short circuits, powerful arcing faults then occur, which must be controlled with regard to the protection of the equipment and above all with regard to the protection of persons when working on open or opened systems. Assessing the risks associated with such arcs requires knowledge of arc voltage, arc current and arc power and, above all, the energy conversion to be expected at potential fault locations in order to be able to initiate or guarantee appropriate and effective protective measures. In the context of personal protection, the thermal hazards of such arcs are of primary importance. In cases where persons may be directly exposed to the arcs, Personal Protective Equipment against the thermal hazards of an electric arc must be used, and its selection must be made in accordance with well-founded procedures. [2]

This article mainly focusses on the comprehensive document with respect to the short-circuit current profiles and protective devices in dc systems, which are very fundamental to the accurate calculations of arc-flash hazard in dc systems. This article provides equations with practical examples of Incident Energy calculations in DC systems and the analysis of arc-flash hazard.

2. DC arc flash for PV system

The diagram illustrates a photovoltaic (PV) system configuration where 16 PV panels are connected to a single inverter. This setup allows the panels to collectively convert solar energy into direct current (DC) electricity, which is then converted into alternating current (AC) by the inverter for use in the electrical grid or for powering appliances. The PV panels are typically connected in series or parallel, depending on the required voltage and current ratings, to optimize energy capture and system efficiency. The inverter plays a crucial role in ensuring that the DC output from the panels is efficiently transformed into a usable AC output, accommodating the system’s voltage and power requirements. The ratings and specifications of both the PV panels and inverter are critical for ensuring that the system operates effectively and meets energy production goals.

2.1 Fundamental Concept for DC Arc Flash

The DC sources can be modelled as constant current or voltage behind impedance. It is recommended to use the voltage behind impedance model whenever possible to obtain more accurate results. The image below represents a battery with a source resistance and a fault at its terminal and also The arc resistance is added to the circuit to represent an actual arc fault scenario. The image below shows the arc resistance and the calculation of the arcing current.

Incident Energy. The amount of thermal energy impressed on a surface, a certain distance from the source, generated during an electrical arc event. Incident energy is typically expressed in calories per square centimetre (cal/cm²). [8]

Once the arc resistance, voltage and current are known, then the arc power and energy can be easily calculated. The following basic equations apply.

The power in the dc or single-phase arcs can be expressed as [3]

Therefore, the arc energy can be calculated from

where t_arc is the arcing time in seconds, I_arc is in amperes, and R_arc in ohms. This gives the energy in watt-seconds or joules. To convert to calories, multiply by a factor of 0.239, as in the following:

The arc duration (t_arc) is measured in seconds. It should be noted that dc arcs do not pass through current zero every half cycle, which makes low voltage (LV) single-phase ac arcs susceptible to self-extinction

3. DC Arc Current Calculation Methods

DC arc flash has two fundamentally different methods to model and determine the dc arc flash current for different types of sources, and in particular for DCPV array systems (Photovoltaic systems).

3.1 DC Arc Current Calculation – Method 1

This first method works well for systems where the dc arc current is mostly coming from voltage behind impedance sources. However, this method may not be accurate enough for systems where the majority of the dc arc current comes from constant current sources.

3.2 DC Shot Circuit and Arc Current Calculation – Method 2

This method was first introduced at the 2015 IEEE / IAS electrical safety workshop in Louisville Kentucky in the form of a tutorial session (“AC & DC Arc Flash Analysis for Renewable Energy Systems”).  This method was added to ETAP dc arc flash in response to a large number of requests for higher accuracy models for DC PV array systems. The main benefits of this method are:

1. It reduces the over conservative approach of the maximum power method since it allows for an actual arc current operating point determined from the PV array P-V short-circuit curves.
2. It is combined with the Stokes and Oppenlander and Paukert methods; which by themselves are considered a “rigorous” or “detailed” calculation method for dc arc flash current.

The following image illustrates the concept of this method. The arc voltage and resistance are determined iteratively by the program. The iterative routine utilizes the PV characteristic short-circuit curves and the (Paukert / Stokes & Oppenlander) equations to determine the final value of the dc arc current.

In the ETAP simulation for the PV system, the arc current is found using Arc Method 2, which is essentially equivalent to the PV panels short circuit current. This value is critical for accurately assessing the arc flash risk and determining the incident energy levels within the system. Since the short circuit current represents the maximum current the PV panels can produce under fault conditions, it serves as a key parameter in evaluating the potential hazards associated with arc flash incidents. This ensures that appropriate safety measures are implemented based on the actual performance characteristics of the PV system.

PV Array Configuration: Number of panels connected in series- 50

Number of panels connected in Parallel- 4

Total Panels  = 50×4=200

Maximum Power P_max  =  V_oc × I_sc=308.8764 W

Total PV Voltage V_pv = 50× V_oc = 1854 V

Total DC Power  P_dc  =200× V_oc × I_sc=  61.77528 kW

I_scpv = P_dc / V_pv 0.03332 kA

LV panel I_sctotal =16× I_scpv= 0.53312 kA

Arc Current =0.53312 kA

This data illustrates the electrical characteristics of the PV array, particularly focusing on the short circuit current which is taken as arc current as per method 2, which is an essential parameter for determining the potential risks and behaviours during fault conditions. This short circuit current is used to assess the arc flash potential in the system.

4. Calculations of Fault Clearing Time

The FCT is one of the major factors which affect the calculation of the incident energy. The FCT is the time required to clear the fault (arc to get extinguished by opening protective devices). This time is determined from the time current characteristic curves (TCCs) or the definite times of each protective device that is considered to be a source protective device (source PD). ETAP classifies protective devices (PDs) as of two types. The first and most important are the source PDs. These are the protective devices that energize the faulted bus, and once disconnected, completely isolate the system from any power source. The other type of protective devices is Load PDs. These are the PDs which carry power to the loads or subsystems connected to a faulted bus, but do not provide power from a source (i.e. battery, battery charger, converters, and etc).

ETAP takes the most conservative approach when determining the fault clearing time (FCT). If there are several parallel source PDs feeding the bus, it will select the longest FCT (or the time at which the last source PD opens). If there is multiple source PDs in series on the same branch, it will take the shortest opening time of such PDs. The FCT is then used to calculate the incident energy for the bus and load PDs.

The arcing time is calculated based on the operating characteristics of the protective device. The dc breakers may have thermal-magnetic or electronic trip Devices The dc breakers can be categorized as follows [8]

1. General-purpose low-voltage (LV) dc power circuit breakers do not limit the peak available current and may not prevent the prospective fault current to rise to its peak value.
2. A high-speed breaker, during interruption, limits the peak to a value that is less than the available (perspective) current, and these breakers have a short-circuit rating and a short-time rating.
3. A semi-high-speed circuit breaker does not limit the short-circuit current on circuits with minimal inductance but becomes current-limiting for highly inductive circuits. This design also requires a peak rating.
4. Rectifier circuit breakers are a class in themselves, and these carry the normal current output of one rectifier. During fault conditions, these function to withstand or interrupt abnormal currents as required. This breaker requires a short-circuit current rating for n − 1rectifiers and a short-time current rating of its own rectifier.
5. Semi-high-speed and high-speed circuit breakers are equipped with direct acting instantaneous elements that are set at no more than four times the circuit breaker continuous current rating or at the maximum setting below the available sustained current of the test circuit. [3]

For example, consider that a 1000-A class L fuse, which is rated for 500 V_dc and an interrupting current of 100 kA, is applied to a common bus that is served by the four dc sources with bolted and arcing current profiles. Based on the time–current-curve plot of the fuse and the arcing circuit profile, the fuse ac current characteristics for the dc short-circuit currents can be considered without any further adjustments. A simple procedure will be used to calculate the operating time based on the incremental change in the arcing current to which the fuse is subjected. Then, take the weighted average to determine the average current to which the fuse is subjected. The range is 0.01 to 2.0 sec, but smaller and longer time durations can be entered directly in User-Defined FCT (sec). In this simulation, FCT is chosen as 2 sec in User-Defined tab.

5. Incident Energy Method

         5.1 Open-Air Arc Exposures: A large battery-bank installation in a nuclear power plant is an example of an open-air dc-arc flash hazard. For this type of exposure, the heat transfer depends on the spherical energy density, where d represents the distance from the arc (in milli meters) [4]

In the open air, the heat transfer depends on the spherical energy density. Based on the radiant heat transfer, we have

         5.2  Arc-in-a-Box Exposures: When a dc arc is initiated within a piece of switchgear, the enclosure tends to have a focusing effect on the incident energy. Wilkins proposed an approach for three-phase ac arcs where the spherical energy density component is replaced by a value E1 that takes into account the focusing effect of an enclosure. In other words, the term E1 also represents the additional energy reflected by the back and sides of the enclosure

When an arc is initiated in an enclosure, it has the focusing effect on the energy. The spherical density component is replaced by value E₁, which takes into account the focusing effect of the enclosure, as in the following:

The values of a and k in are shown in below Table.

6. Equations for Calculation of Incident Energy in DC Systems

There are many methods suggested by the reviewer to calculate incident energy for DC systems, among them the following methods are being used in ETAP. The main factor to be considered for this step would be the type of equipment (enclosed or open-air types). [3]

        6.1 Maximum Power Method:

As per NFPA 70E, this method is based on the concept that the maximum power possible in a dc arc will occur when the arcing voltage is one-half the system voltage. Based on Testing it has shown that this calculation is conservatively high in estimating the arc flash value. This method applies to dc systems rated up to 1000 volts.

Where, I_arc = arcing current, amperes

I_bf = system bolted fault current, amperes

IE_m = estimated dc arc flash incident energy at the maximum power point, cal/cm²

V_sys = system voltage, volts

T_arc = arcing time, sec

R_{arc =} Arc Resistance

 

D = working distance, cm

Note: This input field has a range of 1 to 1000 Volts dc if the Maximum power method is selected. The voltage can be higher than 1000 V dc if the Stokes or Paukert methods are selected. Higher values of voltage can be entered directly. The main problem with this method is that it does not yield accurate arcing current values. In fact it may be better to assume a fault clearing time or incident energy exposure time (i.e. fixed FCT) with this method to determine the energy. Regardless, ETAP still uses the arcing current predicted from this method to determine the clearing time. This calculation is not recommended for system nominal voltages higher than 1000 Volts dc.

6.2 Stokes and Oppenlander   

Stokes and Oppenlander performed perhaps the most exhaustive study of free-burning vertical and horizontal arcs between series electrodes in open air. Stokes and Oppenlander formulated the minimum arc voltages for series electrodes. DC arcs in an industrial setting are likely to be initiated between parallel electrodes, which are characterized by longer arc lengths and higher arc voltages. Stokes and Oppenlander modelled the arc voltage for arcing currents above a transition point. “This set of data, totalling some two million current and voltage points, was reassembled to current–voltage characteristics. These characteristics were compiled into empirical equations which are used by ETAP to determine the arcing current using an iterative method.

The main equation used by ETAP to determine the arcing current is shown below:

Stokes & Oppenlander
Ibf	=533.12		A
Iarc	=533.12		A
Zg	=20		mm
Varc	=65.174		V
Rarc	=0.12225		Ohm
d	=45.72		cm
IE in cal	=16608.38		cal
a	=40		cm
k	=0.312		–
IE close box	=1.404164		cal/cm2

The only way to solve the equations above is iteratively because of their non-linear nature. ETAP only calculates the arcing currents above the transition current I_t. If arcing current is below transition point, a solution cannot be reached and the program will flag this condition.  If the gap, voltage and system impedance are within the limits of the equations, the model can predict if the arc is sustained. If the gap is too long, a solution may not be found. With this method, the arcing current and arc fault duration calculation is more accurate. The incident energy calculated as a result of this method should be more accurate rather than over conservative.

This method requires an iterative solution and because of this it is not easy to calculate manually unlike the maximum power method.

6.3 Paukert Method

Paukert compiled published arcing-fault data from seven researchers who conducted a wide range of arc tests. Some tests were dc, and some tests were ac. Some configurations were vertical, and others were horizontal. Arcing currents ranged from 0.3 A to 100 kA, and electrode gaps ranged from 1 to 200 mm (0.039 to 8 in). Based on the collected data, Paukert formulated arc-voltage and arc-resistance equations for various electrode gap widths; these equations are listed in table shown below. First Table presents an inverse V –I characteristic for low-current arcs and  second Table presents positive V –I characteristic for currents above 100 A.

ETAP determines the arcing current from the equations listed above for different gap values. The following table describes how these equations are selected based on the equipment gaps:

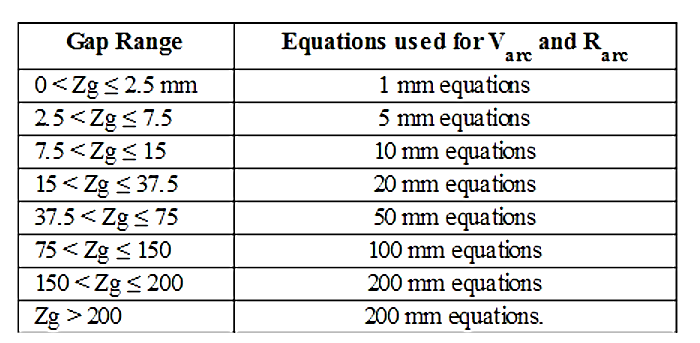
Paukert Method
Varc	=66.29928059	V
Ibf	=0.53312	kA
Iarc	=533.12	A
Rarc	=0.124383574	ohm
IE arc	=16898.21684	cal
a	=40	cm
d	=45.72	cm
k	=0.312	–
IE close box	=1.428669042	Cal/cm2

The compiled test data included DC arcs with both vertical and horizontal electrode configurations. The test also included arcing currents ranging from 0.3A to 100kA and electrode gaps from 1 to 200mm. Similar to the Stokes and Oppenlander method, if the gap voltage and/or system impedance are within the range of the equations, the model can predict if the arc can occur. The arcing current and arc duration from the TCCs is also more accurate when compared to the maximum power method.

The Paukert method may not be applicable for electrode gaps more than 200 mm. however ETAP uses the 200 mm equation to obtain the results. The arcing current used for this model should not exceed 100 kA.

 

The following special condition messages which may be generated in the DC Arc Flash page or by the global DC arc flash calculation as results of method limitations.

6.4 Arc Flash Boundary

A distance from a prospective arc source at which the incident energy is calculated to be 5.0 J/cm² (1.2 cal/cm²). Workers within this boundary need to wear appropriate PPE. The boundary distance helps in setting up safe working zones and barriers.

AFB=0.52 m from Stokes & Oppenlander method

AFB=  0.527 m from Paukert method

6.5 Working Distance

The results of the incident energy calculation can be utilized to define minimum arc thermal performance value or energy breakdown rating of the PPE for personnel working on energized equipment. The distance between the potential arc source and the face and chest of the worker performing the task is considers as 18 inch. The incident energy calculation is sensitive to the working distance; greater distances generally reduce the incident energy exposure. Ensure that the working distance used in the study matches the actual working conditions.

7. Recommendations:

From the above results it is observed that as per NFPA70E, the PPE category must be chosen based on the incident Energy level as follows. For the simulated system, Level 1 PPE category and two types of danger label are advised to follow is shown below,

8. Conclusion

This article has explored the critical aspects of conducting a DC arc flash study, focusing on the key parameters that influence the safety and reliability of electrical systems. We have examined the calculation of short circuit current, arcing time and arcing current each playing a vital role in determining the severity of an arc flash event. The methods of calculating incident energy, including Maximum power method, Stokes & Oppenlander and Paukert’s methods, provide comprehensive insights into the potential hazards present in DC systems. The determination of arc flash boundaries, crucial for defining safe working distances, was discussed in detail, with all boundaries evaluated for photovoltaic (PV) systems. A sample study using ETAP software demonstrated how these calculations can be applied in real-world scenarios, highlighting the importance of aligning software outputs with theoretical expectations. The results analysis confirmed the accuracy and effectiveness of these methodologies, emphasizing the need for thorough DC arc flash studies in any system where DC power is utilized. By understanding and applying these principles, engineers can design safer systems, mitigate risks and ensure the protection of both personnel and equipment.

9. References:

1. S. Weimann, R. J. Kerestes and B. M. Grainger, “Comparative Analysis of Experimental DC Arc Flash Results to Industry Estimation Methods,” in IEEE Open Journal of Industry Applications, vol. 1, pp. 181-193, 2020, doi: 10.1109/OJIA.2020.3031768.
2. Schau and S. Glaser, “Approaches for Calculating LV DC Arc Flash Parameters,” 2020 55th International Universities Power Engineering Conference (UPEC), Turin, Italy, 2020, pp. 1-6, doi: 10.1109/UPEC49904.2020.9209797.
3. DC-Arc Models and Incident-Energy Calculations,”Ammerman, R.F.; et al.; IEEE Transactions on Industry Applications, Vol. 46, No.5.
4. “Arc Flash Calculations for Exposures to DC Systems,”Doan, D.R., IEEE Transactions on Industry Applications, Vol. 46, No.6.
5. “DC Arc Hazard Assessment Phase II”, Copyright Material, Kinectrics Inc., Report No. K-012623-RA-0002-R00.
6. C. Das, “Arc-Flash Hazard Calculations in LV and MV DC Systems Part—II: Analysis,” in IEEE Transactions on Industry Applications, vol. 50, no. 3, pp. 1698-1705, May-June 2014, doi: 10.1109/TIA.2013.2288423.
7. C. Das, “Arc-Flash Hazard Calculations in LV and MV DC Systems—Part I: Short-Circuit Calculations,” in IEEE Transactions on Industry Applications, vol. 50, no. 3, pp. 1687-1697, May-June 2014, doi: 10.1109/TIA.2013.2288416.